Modern Bloom Filters: 22x Faster!

An \((n, \epsilon)-\) Bloom filter \(B\) is an array of \(m\) bits and \(k\) hash functions, where \(m\) and \(k\) are picked in some combination so the false positive rate is at most \(\epsilon\) when the number of inserted elements is at most \(n\). Obviously \(k\) hash functions can be very expensive to evaluate, but luckily Kirsch and Mitzenmacher devised a scheme to compute \(k\) functions from two (specificially $g_i = h₁ + ih₂) (1). In this implementation, we cheat even further by treating a single 64-bit hash as two 32-bit hashes.

struct BasicBloomFilter
{
    int ComputeNumBits();
    int ComputeNumHashFns();

    BloomFilter(int n, float eps) : n(n), epsilon(eps)
    {
        int m = ComputeNumBits();
        bv.resize((m + 7) / 8);
    }

    int n;
    float epsilon;
    std::vector<uint8_t> bv;

    void Insert(uint64_t hash);
    bool Query(uint64_t hash);
};

To insert, we simply evaluate all \(k\) hash functions on the inserted element and set the corresponding bit in the bit vector.

void BasicBloomFilter::Insert(uint64_t hash)
{
    int k = ComputeNumHashFns();
    for(int i = 0; i < k; i++)
    {
        uint64_t bit_pos = ComputeHash(hash, i) % m;
        uint64_t bit_idx = bit_pos % 8;
        uint64_t byte_idx = bit_pos / 8;
        bv[byte_idx] |= (1 << bit_idx);
    }
}

Similarly, to query we just check if all of the corresponding bits are set in the bit vector.

bool BasicBloomFilter::Query(uint64_t hash)
{
    int k = ComputeNumHashFns();
    bool result = true;
    for(int i = 0; i < k; i++)
    {
        uint64_t bit_pos = ComputeHash(hash, i) % m;
        uint64_t bit_idx = bit_pos % 8;
        uint64_t byte_idx = bit_pos / 8;
        result &= (bv[byte_idx] >> bit_idx) & 1;
    }
    return result;
}

For a given \(n, \epsilon\), we'd like to pick \(m, k\) such that \(m\) and \(k\) are minimized while respecting the bound on false positive rate. We can parameterize the relationship between \(\epsilon\) and \(m\) using a bits-per-element metric, \(c = \frac{m}{n}\). It has been shown that for a given \(\epsilon\), the minimum bits per element is \(c = -1.44\log_2{\epsilon}\), with the corresponding number of hash functions being \(k = -\log_2{\epsilon}\). Interestingly, \(k\) is independent of \(n\).

It can also be useful to view \(c\) as the parameter, computing the expected false positive rate. Simply the equation backwards, we get that \(\epsilon = 2^{\frac{c}{-1.44}}\). As you can see below, there are diminishing returns on \(c\) past around \(10\).

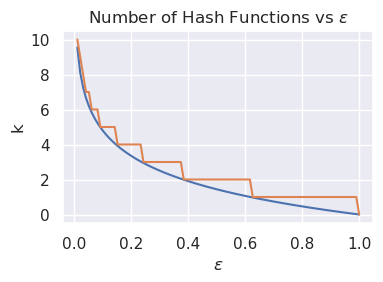
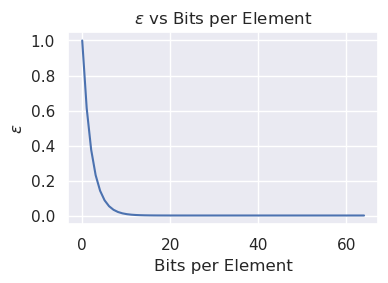
Simply translating these bounds completes the bloom filter:

int BasicBloomFilter::ComputeNumBits()
{
    return static_cast<int>(-1.44 * n * std::log2(epsilon) + 0.5);
}

int BasicBloomFilter::ComputeNumHashFns()
{
    return static_cast<int>(-std::log2(epsilon) + 0.5);
}

I benchmarked the naive algorithm on my i9-9900K (G++ 12.2.0 with -O3, FPR set to 1%, code). The basic Bloom filter costs around 56 cycles/op, going all the way up to around 254 cycles/op on the larger Bloom filters. The false-positive rate does stay right around 1%.

The classic way to deal with cache misses is increasing locality, and Bloom filters are no different. We cannot hope to have fewer than one cache miss per lookup in the general case. However, if each bit lookup after the first happens within a cache line, the only cache miss will be for fetching that cache line. Thus we can divide a Bloom filter into many smaller, cache line-sized Bloom filters called "blocks". The first hash function will index a block, and the other \(k - 1\) functions will operate as in the standard filter.

Take note that the false positive rate of a blocked Bloom filter is higher, as each block has its own \(n\). More precisely, if there are \(b\) blocks, each entry has probability of \(\frac{1}{b}\) of being in a given block. If \(X_{ij}\) is an indicator variable of whether entry \(i\) is in block \(j\), the number of entries in block \(j\) \(n_j = \sum\limits_{i = 1}^{n} X_{ij}\), which implies that \(n_j\) is a random variable following the Binomial distribution \(B(n, \frac{1}{b})\). As such some blocks will be underloaded and others will be overloaded. While the overall effect on space efficiency is not immediately clear, Putze, Felix and Sanders, Peter and Singler, Johannes give a detailed analysis. They show a slight increase in false positive rate, and provide a detailed analysis of the space overhead needed to compensate.

uint8_t *BlockedBloomFilter::GetBlock(uint64_t hash)
{
    int block_idx = ComputeHash(hash, 0) % num_blocks;
    return bv.data() + block_idx * CACHE_LINE_BITS / 8;
}

void BlockedBloomFilter::Insert(uint64_t hash)
{
    int k = ComputeNumHashFns();
    uint8_t *block = GetBlock(hash);
    for(int i = 1; i < k; i++)
    {
        uint64_t bit_pos = ComputeHash(hash, i) % CACHE_LINE_BITS;
        uint64_t bit_idx = bit_pos % 8;
        uint64_t byte_idx = bit_pos / 8;
        block[byte_idx] |= (1 << bit_idx);
    }
}

bool BlockedBloomFilter::Query(uint64_t hash)
{
    int k = ComputeNumHashFns();
    uint8_t *block = GetBlock(hash);
    bool result = true;
    for(int i = 1; i < k; i++)
    {
        uint64_t bit_pos = ComputeHash(hash, i) % CACHE_LINE_BITS;
        uint64_t bit_idx = bit_pos % 8;
        uint64_t byte_idx = bit_pos / 8;
        result &= (1 << bit_idx);
    }
}

The Blocked Bloom filter performs significantly better, hovering right around 30 cycles/op on the low end! Interestingly, probing performance remains constant while build time grows. FPR is less predictable, but seems to remain within 2x of the initial filter (i.e. below 2%).

Unlike the previous Bloom filters, which write bits to memory one at a time, Register-Blocked Bloom filters write all of their bits simultaneously. The filter constructs a mask containing the \(k - 1\) bits (remember one hash is used for the block index) and sets or checks this mask. I won't post the code in this post, but this filter is also straight forward to vectorize, and the benchmarks repository has an AVX2 implementation.

uint64_t *RegisterBlockedBloomFilter::GetBlock(uint64_t hash)
{
    int block_idx = ComputeHash(hash, 0) % num_blocks;
    return reinterpret_cast<uint64_t *>(bv.data()) + block_idx;
}

uint64_t RegisterBlockedBloomFilter::ConstructMask(uint64_t hash)
{
    uint64_t mask = 0;
    for(int i = 1; i < k; i++)
    {
        uint64_t bit_pos = ComputeHash(hash, i) % 64;
        mask |= (1ull << bit_pos);
    }
    return mask;
}

void RegisterBlockedBloomFilter::Insert(uint64_t hash)
{
    uint64_t *block = GetBlock(hash);
    *block |= ConstructMask(hash);
}

bool RegisterBlockedBloomFilter::Query(uint64_t hash)
{
    uint64_t *block = GetBlock(hash);
    uint64_t mask = ConstructMask(hash);
    return (*block & mask) == mask;
}

The register-blocked Bloom filter performs even better than the cache-line-blocked Bloom filter, dipping do just under 20 cycles/op on the small end. However, the FPR has gone up dramatically, to around 5%. To compensate, we can add four extra bits per value, which reduces performance by a few cycles but halves the FPR. Now looking at the SIMD (AVX2) implementation, wow! 5 cycles/op, 4x faster than the non-SIMD version! Since AVX2 doesn't have a mod operator, I had to round the number of blocks to the next power of two so I could use a mask for block selection. I haven't been able to figure out why, but this seems to have impacted the false positive rate by a lot. A histogram of the blocks used (bin size 4) shows a fairly uneven distribution, suggesting some poor interaction with my random number generator.

Before, we were mapping hashes to bit patterns on-the-fly. The bit pattern approach the hash as an index into a table of pre-generated bit patterns. In my implementation, each bit pattern is 57 bits big and has 4-5 bits set. To insert, we simply mask the designated bits of the hash and get the mask from the table. To combat a rise in FPR, the authors of (3) propose a strategy loading several masks from the table and OR-ing them together to achieve a greater variety (Pattern Multiplexing). My good friend Michal had another idea of reserving 6 bits of the hash to give a rotation for the mask (called Mask Rotation), which works well in practice.

The Patterned Bloom Filter requires only one hash, unlike the previous ones which required two, so I've swithced to using a single 64-bit hash. Below I've included a scalar version and an AVX2 version of the mask construction.

uint64_t ConstructMaskScalar(uint64_t hash)
{
    uint64_t mask_idx = hash & ((1 << LogNumMasks) - 1);
    uint64_t mask_rotation = (hash >> LogNumMasks) & ((1 << 6) - 1);
    uint64_t mask = LoadMask(mask_idx);
    return RotateLeft(mask, mask_rotation);
}

void ConstructMaskSIMD(
    __m256i &vecMask,
    __m256i &vecHash)
{
    __m256i vecMaskIdxMask = _mm256_set1_epi64x((1 << LogNumMasks) - 1);
    __m256i vecMaskMask = _mm256_set1_epi64x((1ull << MaskTable::bits_per_mask) - 1);
    __m256i vec64 = _mm256_set1_epi64x(64);

    __m256i vecMaskIdx = _mm256_and_si256(vecHash, vecMaskIdx);
    __m256i vecMaskByteIdx = _mm256_srli_epi64(vecMaskIdx, 3);
    __m256i vecMaskBitIdx = _mm256_and_si256(vecMaskIdx, _mm256_set1_epi64x(0x7));
    __m256i vecRawMasks = _mm256_i64gather_epi64((const long long *)masks.masks, vecMaskByteIdx, 1);
    __m256i vecUnrotated = _mm256_and_si256(_mm256_srlv_epi64(vecRawMasks, vecMaskBitIdx), vecMaskMask);

    __m256i vecRotation = _mm256_and_si256(
        _mm256_srli_epi64(vecHash, mask_idx_bits),
        _mm256_set1_epi64x((1 << rotate_bits) - 1));
    __m256i vecShiftUp = _mm256_sllv_epi64(vecUnrotated, vecRotation);
    __m256i vecShiftDown = _mm256_srlv_epi64(vecUnrotated, _mm256_sub_epi64(vec64, vecRotation));
    vecMask = _mm256_or_si256(vecShiftDown, vecShiftUp);
}

With this final optimization, we've arrived at the "ultimate" Bloom filter: 2.5 cycles/op, with a FPR that's not worse than the non-patterned SIMD Bloom Filter. While this FPR is not bad for some applications, it can be further tuned by increasing the size and number of patterns.